题目描述

最大子段和

给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0。

题目分析

这是一个动态规划问题，从序列第一个元素开始累加，到接下来的元素时，有两种情况，一是累加的结果>=0，这样后面的元素与其相加时，结果是继续变大的。二是累加的结果<0,这时与新的元素相加会让结果变小，就把<0的舍弃，将下一个元素作为累加的新开始。下面用流程图演示一下。

流程图

用visio画的，不知道为什么导出来这么大

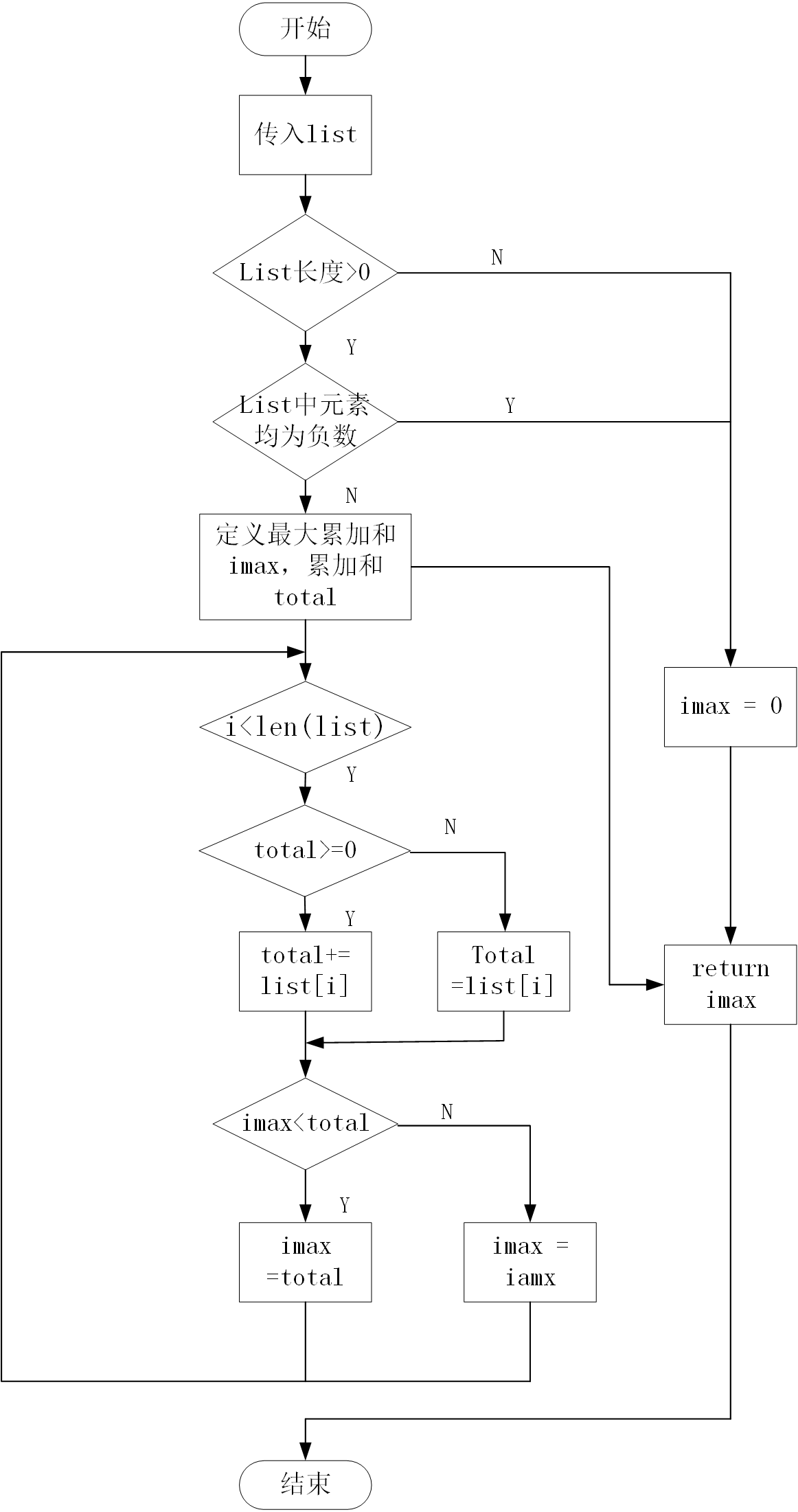
Code

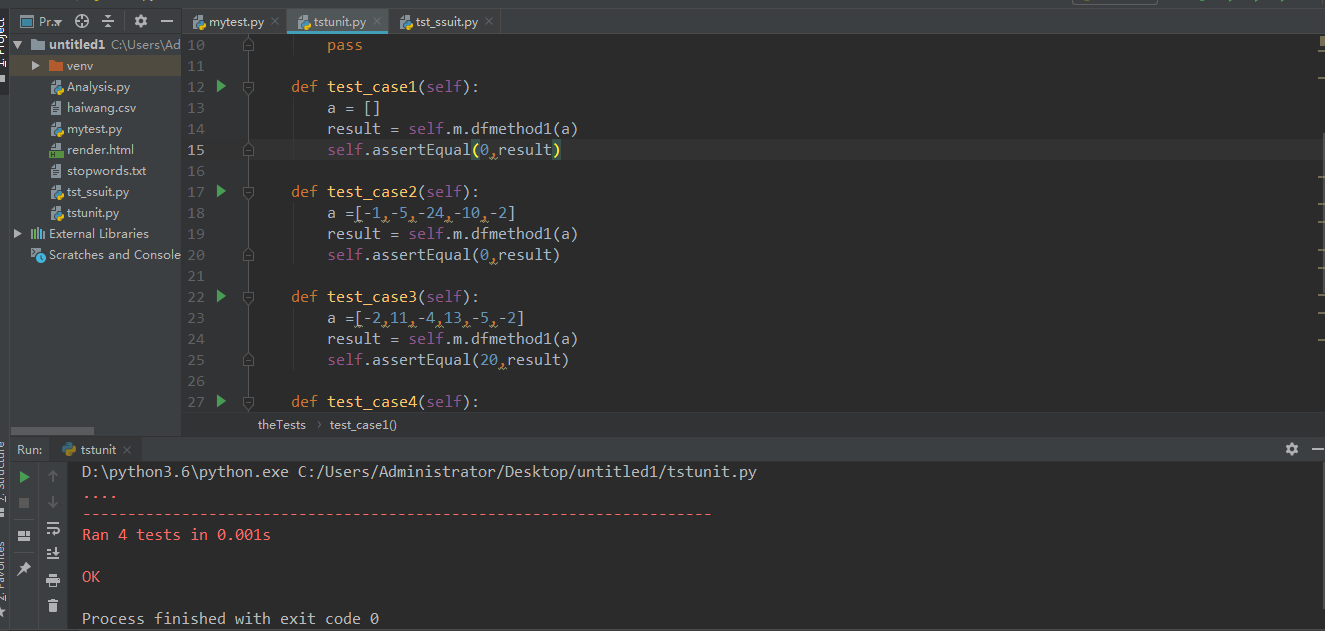
单元测试

判定/条件覆盖测试

要判断的条件：

1.list长度>0?

2.list内是否全为负数(total<0)?

3.累加结果total是否>0?

3.最大和imax是否<total?

这些是我的一些测试样例

样例	满足的条件	应输出的结果
a=[]	len=0	0
a=[-1,-5,-24,-10,-2]	len>0,total<0	0
a=[-2,8,-9,5,-4,6]	len>0,total>imax,total先<0后>0	8
a=[-2,11,-4,13,-5,-2]	len>0,total<imax	20

Code

测试结果

四个.说明测试通过

下面有什么呢？